The vertical force F acts downward at A on the twomembered frame. Determine the magnitudes of the twocomponents of F directed along the axes of AB and AC.Set F = 500 N.

Step-by-Step Solution

Step 1

We are given the value of force $F = {\rm{500 N}}$.

We are asked to estimate the magnitudes of the two components of F.

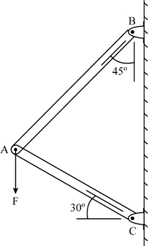
Step 2

The following is the free body diagram to calculate the magnitude of force related to link AB.

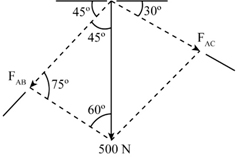
To find the magnitude of force we will use the law of sines.\[\frac{{{F_{AB}}}}{{\sin 60^\circ }} = \frac{F}{{\sin 75^\circ }}\]

Plugging the known values in the above equation.\[\begin{array}{c} \frac{{{F_{AB}}}}{{\sin 60^\circ }} = \frac{{500\;{\rm{N}}}}{{\sin 75^\circ }}\\ {F_{AB}} = 448.28\;{\rm{N}} \end{array}\]

Step 3

The following is the free body diagram to calculate the magnitude of force related to link AB.

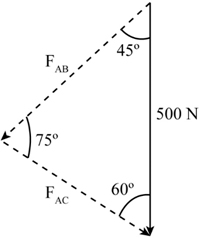
To find the magnitude of force we will use the law of sines.\[\frac{{{F_{AC}}}}{{\sin 45^\circ }} = \frac{F}{{\sin 75^\circ }}\]

Plugging the known values in the above equation.\[\begin{array}{c} \frac{{{F_{AC}}}}{{\sin 45^\circ }} = \frac{{500\;{\rm{N}}}}{{\sin 75^\circ }}\\ {F_{AC}} = 366.02\;{\rm{N}} \end{array}\]