Share
Letf(x,y),0≤ x, y ≤ 1,satisfythefollowing conditions: for each x, f(x,y) is an integrable function of y,and(∂f(x,y)/∂x) is a bounded function of (x, y). Show that (∂f(x,y)/∂x) is a measurable function of y for each x and d dx 1 0 1 f (x, y)dy = 0 ∂ ∂x f(x,y)dy.
ReportQuestion
Please briefly explain why you feel this question should be reported.
Letf(x,y),0≤ x, y ≤ 1,satisfythefollowing conditions: for each x, f(x,y) is an integrable function of y,and(∂f(x,y)/∂x) is a bounded function of (x, y). Show that (∂f(x,y)/∂x) is a measurable function of y for each x and d dx 1 0 1 f (x, y)dy = 0 ∂ ∂x f(x,y)dy.
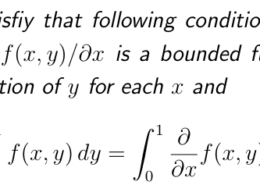
Leave an answer