Step-by-Step Solution
Step 1
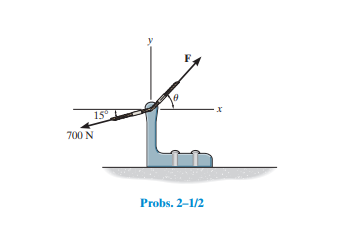
We are given the force ${F_R} = 500\;{\rm{N}}$ and ${F_1} = 700\;{\rm{N}}$.
We are asked to determine the magnitude of force ${\bf{F}}$ and its direction ${\bf{\theta }}$.
Step 2
The following is the diagram of the vector component.

The following is the diagram of the vector component tail to tail.
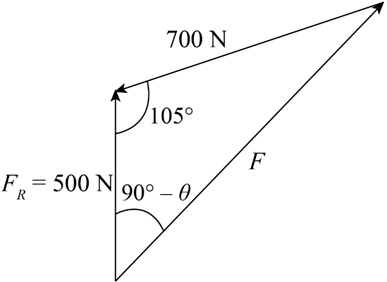
Step 3
To find the magnitude of force we will use the relation from cosines law.\[{\bf{F}} = \sqrt {{F_1}^2 + {F_R}^2 – \left( {2{F_1}{F_R} \times \cos 105^\circ } \right)} \]
On plugging the values in the above relation we get,\[\begin{array}{c} {\bf{F}} = \sqrt {{{\left( {700\;{\rm{N}}} \right)}^2} + {{\left( {500\;{\rm{N}}} \right)}^2} – \left( {2 \times 500\;{\rm{N}} \times 700\;{\rm{N}} \times \cos 105^\circ } \right)} \\ {\bf{F}} = \sqrt {921173.33} \;{\rm{N}}\\ {\bf{F}} = 959.7\;{\rm{N}} \end{array}\]
To find the direction of force we will use the relation from sines law.\[\frac{{\sin \left( {90^\circ + {\bf{\theta }}} \right)}}{{{F_1}}} = \frac{{\sin 105^\circ }}{{\bf{F}}}\]
On plugging the values in the above relation we get,\[\begin{array}{c} \frac{{\sin \left( {90^\circ + {\bf{\theta }}} \right)}}{{700\;{\rm{N}}}} = \frac{{\sin 105^\circ }}{{959.7\;{\rm{N}}}}\\ \sin \left( {90^\circ + {\bf{\theta }}} \right) = \frac{{\left( {700\;{\rm{N}}} \right) \times \sin 105^\circ }}{{959.7\;{\rm{N}}}}\\ \left( {90^\circ + {\bf{\theta }}} \right) = {\sin ^{ – 1}}\left( {0.704} \right)\\ {\bf{\theta }} = 45.26^\circ \end{array}\]