Consider a Shallow neural network with the following parameters. ϕ = {ϕ0, ϕ1, ϕ2, ϕ3, θ10, θ11, θ20, θ21, θ30, θ31} = {−0.23,−1.3, 1.3, 0.66,−0.2, 0.4,−0.9, 0.9, 1.1,−0.7}. Assuming the following activation functions, draw the input-output relationship highlighting the linear regions.

Report
Question

Please briefly explain why you feel this question should be reported.

Report
Cancel

Consider a Shallow neural network with the following parameters.
ϕ = {ϕ0, ϕ1, ϕ2, ϕ3, θ10, θ11, θ20, θ21, θ30, θ31} = {−0.23,−1.3, 1.3, 0.66,−0.2, 0.4,−0.9, 0.9, 1.1,−0.7}.
Assuming the following activation functions, draw the input-output relationship highlighting the linear regions.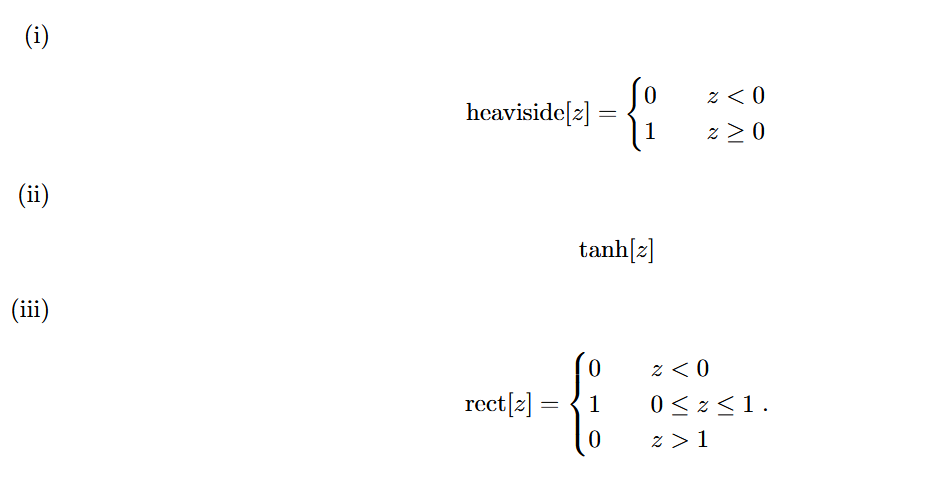

 

in progress 0
dp 2025-03-23T09:29:10+05:00 3 Answers 9 views Beginner
0
MathJax Example

Answers ( 3 )

  1. Admin
    0
    2025-03-23T15:50:26+05:00
    Report Reply

    Please briefly explain why you feel this answer should be reported.

    Report
    Cancel

  2. Admin
    0
    2025-03-23T16:02:48+05:00
    Report Reply

    Please briefly explain why you feel this answer should be reported.

    Report
    Cancel

  3. MathJax Example
  4. Admin
    0
    2025-03-23T16:07:12+05:00
    Report Reply

    Please briefly explain why you feel this answer should be reported.

    Report
    Cancel
    /import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # Import for 3D plotting

# Define the ReLU function
def relu(z):
    return np.maximum(0, z)

# Define the Heaviside function
def heaviside(z):
    return np.heaviside(z, 1)

# Define the Rect function
def rect(z):
    return np.piecewise(z, [z < 0, (z >= 0) & (z <= 1), z > 1], [0, 1, 0])

# Define the network parameters
phi = [-0.23, -1.3, 1.3, 0.66]
theta = [[-0.2, 0.4], [-0.9, 0.9], [1.1, -0.7]]

# Create a figure with subplots
fig = plt.figure(figsize=(12, 10))
fig.suptitle("Activation Functions and Shallow Neural Network Output")

# Plot 1: Heaviside Function
ax1 = fig.add_subplot(2, 2, 1)
z = np.linspace(-2, 2, 1000)
y_heaviside = heaviside(z)
ax1.plot(z, y_heaviside, label="Heaviside Function", color="blue")
ax1.set_title("Heaviside Function")
ax1.set_xlabel("z")
ax1.set_ylabel("heaviside[z]")
ax1.grid()
ax1.legend()

# Plot 2: Tanh Function
ax2 = fig.add_subplot(2, 2, 2)
y_tanh = np.tanh(z)
ax2.plot(z, y_tanh, label="Tanh Function", color="green")
ax2.set_title("Tanh Function")
ax2.set_xlabel("z")
ax2.set_ylabel("tanh[z]")
ax2.grid()
ax2.legend()

# Plot 3: Rect Function
ax3 = fig.add_subplot(2, 2, 3)
y_rect = rect(z)
ax3.plot(z, y_rect, label="Rect Function", color="red")
ax3.set_title("Rect Function")
ax3.set_xlabel("z")
ax3.set_ylabel("rect[z]")
ax3.grid()
ax3.legend()

# Plot 4: Shallow Neural Network Output
ax4 = fig.add_subplot(2, 2, 4, projection='3d')  # Create a 3D subplot
x1 = np.linspace(-2, 2, 100)
x2 = np.linspace(-2, 2, 100)
X1, X2 = np.meshgrid(x1, x2)
Y = np.zeros_like(X1)

# Compute the output for each input pair
for i in range(len(x1)):
    for j in range(len(x2)):
        h1 = relu(theta[0][0] + theta[0][1] * X1[i, j])
        h2 = relu(theta[1][0] + theta[1][1] * X1[i, j])
        h3 = relu(theta[2][0] + theta[2][1] * X1[i, j])
        Y[i, j] = phi[0] + phi[1] * h1 + phi[2] * h2 + phi[3] * h3

# Plot the output as a surface
surf = ax4.plot_surface(X1, X2, Y, cmap='viridis')
ax4.set_title("Shallow Neural Network Output")
ax4.set_xlabel("x1")
ax4.set_ylabel("x2")
ax4.set_zlabel("y")
fig.colorbar(surf, ax=ax4, shrink=0.5, aspect=5)

# Adjust layout and show plots
plt.tight_layout()
plt.show()/

Leave an answer

Browse

By answering, you agree to the Terms of Service and Privacy Policy.