Step-by-Step Solution
Step 1
Given that the angle $\theta $ is $60^\circ $, and the force $F = 450\;{\rm{N}}$.
We are required to determine the resultant force and its direction measured counter clockwise from the positive $x$ -axis.
Step 2
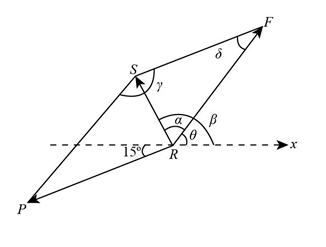
We have to make the parallel lines from the force vectors to get a parallelogram. The parallelogram is shown below.
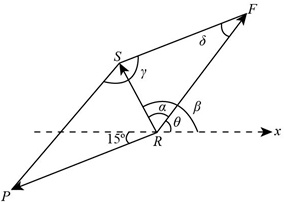
Step 3
By the geometry, we can determine the angle between the forces. The angle between the forces can be calculated as,\[\begin{array}{c} {a_n} = 180^\circ – 60^\circ + 15^\circ \\ = 135^\circ \end{array}\]
Step 4
We shall now, use the law of cosine to calculate the resultant force. The law of cosine can be written as,\[{F_R} = \sqrt {F{R^2} + P{R^2} – 2 \times \left( {FR} \right) \times \left( {PR} \right)\cos \left( {180^\circ – {a_n}} \right)} \]
Step 5
Substitute all the values in the above equation.
\[\begin{array}{c} {F_R} = \sqrt {{{\left( {450\;{\rm{N}}} \right)}^2} + {{\left( {700\;{\rm{N}}} \right)}^2} – 2 \times \left( {450\;{\rm{N}}} \right) \times \left( {700\;{\rm{N}}} \right) \times \cos \left( {180^\circ – 135^\circ } \right)} \\ = 497.0\;{\rm{N}} \end{array}\]
Step 6
The angle $\delta $ can be calculated as,
\[\delta = \frac{{360^\circ – 2 \times {a_n}}}{2}\]
Step 7
Substitute all the values in the above equation.
\begin{array}{c} \delta = \frac{{360^\circ – 2 \times 135^\circ }}{2}\\ = 45^\circ \end{array}
Step 8
Now, we shall apply the sine law to calculate the angle $\alpha $. The sine rule is given by,
\begin{array}{c} \frac{{\sin \alpha }}{{RP}} = \frac{{\sin \delta }}{{RS}}\\ \sin \alpha = \frac{{RP \times \sin \delta }}{{RS}}\\ \alpha = {\sin ^{ – 1}}\left( {\frac{{RP \times \sin \delta }}{{RS}}} \right) \end{array}
Step 9
Substitute all the values in the above equation.
\begin{array}{c} \alpha = {\sin ^{ – 1}}\left( {\frac{{700\;{\rm{kN}} \times \sin 45^\circ }}{{497\;{\rm{N}}}}} \right)\\ = 84.8^\circ \\ \approx 58.6^\circ \end{array}
Step 10
The angle measured anticlockwise from the $x$ -axis can be calculated as,\begin{array}{c} \lambda = \alpha + 60^\circ \\ = 58.6^\circ + 60^\circ \\ = 118.6^\circ \end{array}